
Julia Set
Fractals
 |
Making Julia Set Fractals |
Most of the 2D fractal images used in this
website and in my book are called
Julia sets, named for the early twentieth century French mathematician
Gaston Julia, who pioneered the method by which they are produced.
The method is not difficult to understand, provided you have enough
background. A good course in Algebra II is more than enough math to cover
all of the topics used to produce these images. But without a semester or
two for study, let me offer the reader some of the important technical highlights
before describing how the computer actually produces the images. For the
layman, I strongly suggest a thorough and repeated reading throughout
this section to achieve the desired comprehension.
First, you'll need to know what a square
root is. We say that the square root
of 25 is 5 or -5 because both 5 times
5 and -5 times -5 equals 25. Likewise the
square root of 81 is 9 or -9. This is all very normal and proper.
But a strange thing occurs when we try to
take the square root of a negative
number like -4. After all, 2 times 2 equals 4 and -2 times -2 equals 4. To work
around this uncomfortable situation, mathematicians use an imaginary
number
to represent the square root of a negative number. We say that the square root
of -1 is i; that means that i times i
equals -1. What is the square root of -9? Why 3i
(or -3i) of course. Numbers like 3i, -74i, 8.6i and i itself are called imaginary
numbers.
Though they do not exist in the realm of real numbers,
these imaginary numbers
play a vital role in physical and engineering calculations as well as in the
generation
of Julia and Mandelbrot set fractals.
Now we can add (or subtract) real numbers
like 7, 43, 2/5, and -9.6 to imaginary
numbers to form complex numbers like 4 + 6i or
-18 - .2i. The complex number set
contains both the real number set and the imaginary number set.
If you can remember back to junior high or
high school, you learned how to
graph an equation by plotting points at their coordinates on a grid and then
connecting the points. Some were straight lines and some were curves.
That grid was called the Cartesian plane (after
René Descartes) and had two axes.
The x-axis went left to right and the y-axis went bottom to top as it went from
negative to positive values along its length. The generation of Julia set fractals
are done on a coordinate plane like this one except that the plane is called
the
complex plane (originally called the Argand
plane for the originator of the idea)
and the axes are now the real axis (x) and the imaginary axis (y). The real
axis
represents the real part of a complex number and the imaginary represents the
imaginary part of a complex number. Thus the complex number 2 + 3i would be
plotted two units to the right of center and three units up from there. See
below.
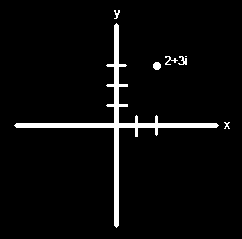 |
Let us now discuss the idea of functions.
A function is sort of a mathematical machine.
You put a number into the machine and you get another number out of the machine.
A function might tell you to double a number and then add three to that number.
It is written as f(x) = 2x + 3 and read as "f of x equals two x plus three,"
where the x
represents whatever number we choose to put into this function. Thus if we put
6 into
our function we get 2 times 6 plus 3 or 15 as the result. If our input value
is 57, our output
value would be 117 and so on. We can then write f(6) = 15 and f(57) = 117. In
this case
the function and its variable x are both in the realm of the real numbers. When
we
generate Julia set fractals, we use functions of a complex
variable. The convention
has been to use the letter z to represent a complex number or variable.
As before,
a complex variable is the sum of a real variable and an imaginary variable.
That is, z = x + yi.
One of the remarkable things about working
with complex numbers is that, outside of
a very few exceptions, no matter what mathematical function you perform on a
complex
number, you always get a complex number as the result. You can add, subtract,
multiply,
or divide them. You can exponentiate them, take any root, or use any of the
trigonometric
functions and you will get a complex number as the result.
The simplest function we use to generate
a Julia set fractal is the function f(z) = z^2 + c.
This means that we would put in a complex number z (which is really x + yi),
then multiply
it by itself (a process called squaring a number),
and then add another complex number c
to the result. The c is a complex constant, that
is, a number that does not change throughout
the entire fractal calculation.
Here is how one of these calculations goes:
Let z = 2 + 3i and c = 4 + 5i. Then*
f(z) = z^2 + c =
= [(2 + 3i) X (2 + 3i)] + (4 + 5i) =
= [(2 X 2) + (2 X 3i) + (3i X 2) + (3i X 3i)] + (4 + 5i) =
= [4 + 6i + 6i + (-9)] + (4 + 5i) =
= (-5 + 12i) + (4 + 5i) =
= -1 + 17i
So f(z) = f(2 + 3i) = (2 + 3i)^2 + (4 + 5i) = -1 + 17i.
*We
normally use a dot to signify multiplication in algebra as "x" might
be confused
with the variable x, but because of the limitations of web publishing, we'll
use capital X.
There are an infinite number of functions
that can be devised. The procedure for
each is essentially the same, except that the operations involved within the
function
will be more complicated and numerous.
The next thing you need to know is how to
find the size or norm of a complex number.
The size or norm of a real number is just the number itself, that is, the norm
of 7 is 7.
But the size of a complex number is found a bit differently:
norm of z = ||z|| = ||x + yi|| = sqrt(x^2 + y^2 ) where sqrt means "square root"
As an example we have:
||3- 4i|| = sqrt(3^2 + (-4)^2) = sqrt(9 + 16) = sqrt(25) = 5.
Notice that the norm is always a real number.
Now one more topic before we get into what
the computer does. Let us visualize the
complex plane: picture a grid with +X (real axis) to the right, -X to the left,
+Y (imaginary
axis) going up, and -Y going down. This grid is the model we program our computer
to graph upon. I usually begin as above and break the screen into 900 divisions
by
900 divisions (because the largest square my monitor displayed in the beginning
(1988)
was 900 by 900 individual color dots or pixels).
This means there are 810,000 points
on our graph/grid corresponding to the 810,000 pixels that my monitor will display.
Of course, the number of points your computer screen can display usually determines
how fine you can divide the graph that you begin from. Each one of these 810,000
points
has numerical coordinates corresponding to their location on the graph. These
coordinates become the starting values of x + yi for inputting values into our
function.
Let's finally describe the actual steps of the computer's program as an algorithm:
1) User input step: Tell the computer what
equation to use, what will be our value
for our complex constant c, how big will our coordinate plane be, our "blowup
parameter," the maximum number of iterations
allowed, and the color map we wish
the computer to display its results in.
2) The computer starts with its upperleftmost
point and its coordinates. In a general
case, the coordinates would be (-1, 1), but we set the computer up to understand
that this is the point (-1 , -1). These are the values for x and y that we plug
into our function.
3) The computer does to those coordinate
values whatever the particular function
you chose specifies it to do. In the simplest case, it would square the complex
number
(-1 - i) and add whatever value for c you inputted in step 1.
4) Then the computer finds the size or norm
of the outputted complex number result
and compares it with the "blowup" parameter.
5) If the norm of the outputted result is
not larger than the "blowup" value, the outputted
x and y values become our new inputted values to the function the next
time around.
We repeat steps 3 thru 5 over and over until the outputted norm is larger than
the
"blowup" parameter. In the meantime, we must keep track of the number
of cycles,
or iterations, it takes for the output to exceed our "blowup" value.
Usually if the
outputted norm does not exceed this value in 256 cycles, we stop calculating
and
call its iteration number 256.
6) Once the size of the outputted value exceeds
our blowup value, we stop calculating,
and we record the number of cycles it took to exceed this blowup value as the
original
point's iteration number.
7) The number of cycles or iterations is
the crucial number for telling the computer
what color to print for that very first point on our graph and screen. Say that
it took 56
iterations for that first point to exceed the blowup value. The computer might
plot that
point red (the actual color depends on the color map you chose). If it only
took 55 iterations,
the computer might be instructed to plot a slightly lighter shade of red. If
it took only 54,
a lighter shade still.
8) Then we return to step 2 above to begin
once anew with the very next point (and its
coordinates) on the screen and repeat steps 3 thru 7 for every one of the 810,000
points
on the screen. Once iteration numbers are calculated for each point and pixels
are colored
appropriately, a picture emerges. You can now see how it can take up to 900
x 900 x 256 =
200,000,000+ calculations for each fractal image. Furthermore, we have only
described
the simplest of functions! (If you are interested in seeing some of the hundreds
of functions
we have researched so far, go HERE.)
This is just the basic procedure for calculating
Julia sets. One thing we have not described
is the importance of the complex number c that we introduced when we started
talking
about complex functions. Remember that as a complex number it too is the sum
of a real
number and an imaginary number. This complex number ostensibly acts as a "seed
value"
and remains constant throughout the entire 200 million possible calculations
for each
fractal image. Interestingly, though the function we choose determines what
family of
images we will get, it is this value c that determines what picture we will
get within that family.
It turns out that certain values of c yield
very plain, stable images of two or three colors
whereas other values of c produce wildly chaotic images involving all 256 colors
and more.
Finding the interesting values of c is crucial to making intriguing Julia set
fractals. We use a
related fractal called the Mandelbrot set
for each function we use, to first find the interesting
values of c. There is only one Mandelbrot set for each complex function but
there is an infinite
number of possible Julia sets. But do not be fooled; within the depths of each
Mandelbrot set
is another infinitude of interesting fractal images just waiting to be uncovered.
The Mandelbrot
set is derived in a very similar way to a Julia set except that the complex
constant c used in
the Julia set calculation is replaced by the actual complex coordinate of each
point being
determined in turn.
Fractal objects and images all exhibit the
quality of self-similarity. That is, if you were
to focus
in on a small portion of a fractal object like the Mandelbrot set and continue
to magnify it,
you would uncover objects that are exactly like the original set. This process
of self-similarity
goes on to infinity within each and every fractal image.
Please consult an algebra book for definitions of those terms in blue print.